Mutual inductance and basic operation

Mutual inductance and basic operation

Suppose we were to wrap a coil of insulated wire around a loop of ferromagnetic material and energize this coil with an AC voltage source:

As an inductor, we would expect this iron-core coil to oppose the applied voltage with its inductive reactance, limiting current through the coil as predicted by the equations X_L = 2pfL and I=E/X (or I=E/Z). For the purposes of this example, though, we need to take a more detailed look at the interactions of voltage, current, and magnetic flux in the device.

.
(adsbygoogle = window.adsbygoogle || []).push({});

Kirchhoff's voltage law describes how the algebraic sum of all voltages in a loop must equal zero. In this example, we could apply this fundamental law of electricity to describe the respective voltages of the source and of the inductor coil. Here, as in any one-source, one-load circuit, the voltage dropped across the load must equal the voltage supplied by the source, assuming zero voltage dropped along the resistance of any connecting wires. In other words, the load (inductor coil) must produce an opposing voltage equal in magnitude to the source, in order that it may balance against the source voltage and produce an algebraic loop voltage sum of zero. From where does this opposing voltage arise? If the load were a resistor, the opposing voltage would originate from the "friction" of electrons flowing through the resistance of the resistor. With a perfect inductor (no resistance in the coil wire), the opposing voltage comes from another mechanism: the reaction to a changing magnetic flux in the iron core.

Michael Faraday discovered the mathematical relationship between magnetic flux (F) and induced voltage with this equal:

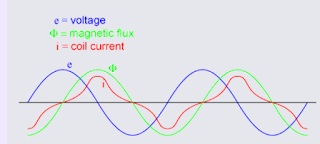
The instantaneous voltage (voltage dropped at any instant in time) across a wire coil is equal to the number of turns of that coil around the core (N) multiplied by the instantaneous rate-of-change in magnetic flux (dF/dt) linking with the coil. Graphed, this shows itself as a set of sine waves (assuming a sinusoidal voltage source), the flux wave 90^olagging behind the voltage wave:

Magnetic flux through a ferromagnetic material is analogous to current through a conductor: it must be motivated by some force in order to occur. In electric circuits, this motivating force is voltage (a.k.a. electromotive force, or EMF). In magnetic "circuits," this motivating force is magnetomotive force, or mmf. Magnetomotive force (mmf) and magnetic flux (F) are related to each other by a property of magnetic materials known as reluctance(the latter quantity symbolized by a strange-looking letter "R"):

In our example, the mmf required to produce this changing magnetic flux (F) must be supplied by a changing current through the coil. Magnetomotive force generated by an electromagnet coil is equal to the amount of current through that coil (in amps) multiplied by the number of turns of that coil around the core (the SI unit for mmf is the amp-turn). Because the mathematical relationship between magnetic flux and mmf is directly proportional, and because the mathematical relationship between mmf and current is also directly proportional (no rates-of-change present in either equation), the current through the coil will be in-phase with the flux wave:

This is why alternating current through an inductor lags the applied voltage waveform by 90^o: because that is what is required to produce a changing magnetic flux whose rate-of-change produces an opposing voltage in-phase with the applied voltage. Due to its function in providing magnetizing force (mmf) for the core, this current is sometimes referred to as the magnetizing current.

distortion

It should be mentioned that the current through an iron-core inductor is not perfectly sinusoidal (sine-wave shaped), due to the nonlinear B/H magnetization curve of iron. In fact, if the inductor is cheaply built, using as little iron as possible, the magnetic flux density might reach high levels (approaching saturation), resulting in a magnetizing current waveform that looks something like this:

When a ferromagnetic material approaches magnetic flux saturation, disproportionately greater levels of magnetic field force (mmf) are required to deliver equal increases in magnetic field flux (F). Because mmf is proportional to current through the magnetizing coil (mmf = NI, where "N" is the number of turns of wire in the coil and "I" is the current through it), the large increases of mmf required to supply the needed increases in flux results in large increases in coil current. Thus, coil current increases dramatically at the peaks in order to maintain a flux waveform that isn't distorted, accounting for the bell-shaped half-cycles of the current waveform in the above plot.

.

ex..citing current

The situation is further complicated by energy losses within the iron core. The effects of hysteresis and eddy currents conspire to further distort and complicate the current waveform, making it even less sinusoidal and altering its phase to be lagging slightly less than 90^o behind the applied voltage waveform. This coil current resulting from the sum total of all magnetic effects in the core (dF/dt magnetization plus hysteresis losses, eddy current losses, etc.) is called the exciting current. The distortion of an iron-core inductor's exciting current may be minimized if it is designed for and operated at very low flux densities. Generally speaking, this requires a core with large cross-sectional area, which tends to make the inductor bulky and expensive. For the sake of simplicity, though, we'll assume that our example core is far from saturation and free from all losses, resulting in a perfectly sinusoidal exciting current.

As we've seen already in the inductors chapter, having a current waveform 90^o out of phase with the voltage waveform creates a condition where power is alternately absorbed and returned to the circuit by the inductor. If the inductor is perfect (no wire resistance, no magnetic core losses, etc.), it will dissipate zero power.